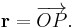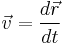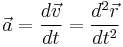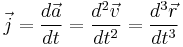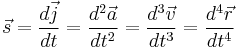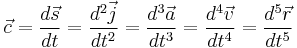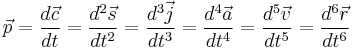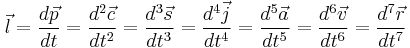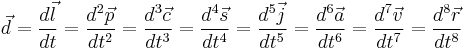Position (vector)
In geometry, a position, location, or radius vector, usually denoted 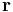 , is a vector which represents the position of a point P in space in relation to an arbitrary reference origin O. It corresponds to the displacement from O to P:
, is a vector which represents the position of a point P in space in relation to an arbitrary reference origin O. It corresponds to the displacement from O to P:
The concept typically applies to two- or three-dimensional space, but can be easily generalized to Euclidean spaces with a higher number of dimensions.[1]
Contents |
Applications
- In linear algebra, a position vector can be expressed as a linear combination of basis vectors.
- The kinematic movement of a point mass can be described by a vector-valued function giving the position
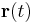 as a function of the scalar time parameter t. These are used in mechanics and dynamics to keep track of the positions of particles, point masses, or rigid objects.
as a function of the scalar time parameter t. These are used in mechanics and dynamics to keep track of the positions of particles, point masses, or rigid objects.
- In differential geometry, position vector fields are used to describe continuous and differentiable space curves, in which case the independent parameter needs not be time, but can be (e.g.) arc length of the curve.
Derivatives of Position
Velocity
Acceleration
Jolt/Jerk/Surge/Lurch
Snap/Jounce
Crackle/Trounce
Pop/Pounce
Lock
Drop
Where 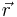 is the position vector,
is the position vector, 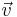 is the velocity vector,
is the velocity vector, 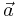 is the acceleration vector,
is the acceleration vector, 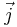 is the jerk vector,
is the jerk vector, 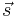 is the snap vector,
is the snap vector, 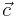 is the crackle vector,
is the crackle vector, 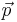 is the pop vector,
is the pop vector, 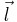 is the lock vector, and
is the lock vector, and 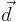 is the drop vector.
is the drop vector.
Relationship to displacement vectors
A displacement vector can be defined as the action of uniformly translating spatial points in a given direction over a given distance. Thus the addition of displacement vectors expresses the composition of these displacement actions and scalar multiplication as scaling of the distance. With this in mind we may then define a position vector of a point in space as the displacement vector mapping a given origin to that point. Note thus position vectors depend on a choice of origin for the space, as well as displacement vectors depend on the choice of an initial point.
See also
Notes
- ^ Keller, F. J, Gettys, W. E. et al. (1993), p28-29
References
- Keller, F. J, Gettys, W. E. et al. (1993). "Physics: Classical and modern" 2nd ed. McGraw Hill Publishing